Rocket Altitude Estimator - Denneth's Awesome Website

The Program

Rocket Estimation, Altitude CalculatoR, or REACT, is a small program I wrote to give a quick and rough estimation of a rocket’s flight performance

The formulas are ~~blatantly stolen~~ from Richards nakka’s .PDF on the subject

First, the program itself

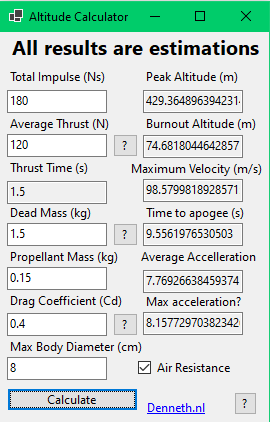
Now basically, all you need to do is enter some statistics, estimations or guesses about your rocket, and you get a estimate for how high it could go, how fast, and how long it would be in the air

The formulas used to get this are not the most accurate way to calculate altitude, but they are simple, so I used them

Speaking of which

The Maths

First, lets define some values

let $F$ be the motor’s average thrust
let $I_t$ be total impulse
let $s$ be the thrust time, which is calculated from $s = I_t / F$
let $m_d$ be the rockets dead mass (no propellant)
let $m_p$ be the propellant mass
let $m$ be the average mass, decided by $m = m_d + \sfrac{1}{2} \: m_p$
let $g$ be the gravitational constant
let $C_d$ be the drag coefficient
let $D$ be the max rocket diameter

With that out of the way, lets see the first formula, which gives the burnout altitude with zero drag

$Z_{1} = \frac{1}{2} \left (\frac{F}{m}-g \right )t^{2}$

(How all this works, why these formulas are used, and example calculations can be found better explained by nakka in his document)

From this, velocity at burnout can be calculated (with zero drag)

$V_{1} = \sqrt{\frac{2 \: Z_{1}}{m}\left (F - m \: g \right )}$

Peak altitude can also be deduced (again assuming zero drag)

$Z_2 = \frac{F \: Z_1}{m \: g}$

And lastly, time to apogee (zero drag, apogee being the highest point reached)

$t_2 = t + \sqrt{\frac{2}{g}\left ( Z2 - Z1 \right )}$

If one also wants to account for air resistance, one can calculate their drag influence number, defined as such

$N = \frac{C_d \: D^{2} \: V1^{2}}{1000 - m_d}\$

Using the provided chart (which has been painstakingly transcribed to .CSV for use in the program) the drag reduction factor can be found

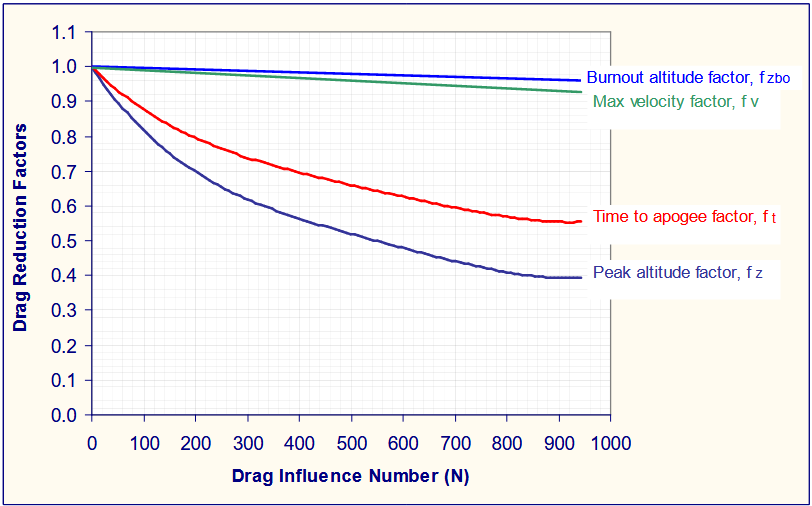
This is then multiplied with the results

$Z_p_e_a_k = f_Z \: Z_2$ Peak altitude, corrected for drag
$Z_b_u_r_n_o_u_t = f_z_b_o \: Z_1$ Burnout altitude, corrected for drag
$V_m_a_x = f_v \: V_1$ Maximum velocity, corrected for drag
$t_p_e_a_k = f_t \: t_2$ Time to apogee, corrected for drag

Further there are 2 formulas provided to calculate average and maximum acceleration

$a = \frac{F}{m \: g}$

$a_m_a_x = \frac{F_m_a_x}{m_d \: g}$

That last one uses $F_m_a_x$ , which I honestly don’t quite understand, but a guess at the formula is included in the program

Now, these formulas only produce estimates, and my implementation is far from perfect

A perfect (and trustworthy) calculator was not the intended result, I just wanted to program something and was using these formulas for calculations anyway

Please keep this in mind when using this, do further research and take nothing for granted

Downloads

As always, source code is available over at github, with binaries also available here

If you found this program useful, found a problem or have any other questions, feel free to contact me

2 thoughts on “Rocket Altitude Estimator”

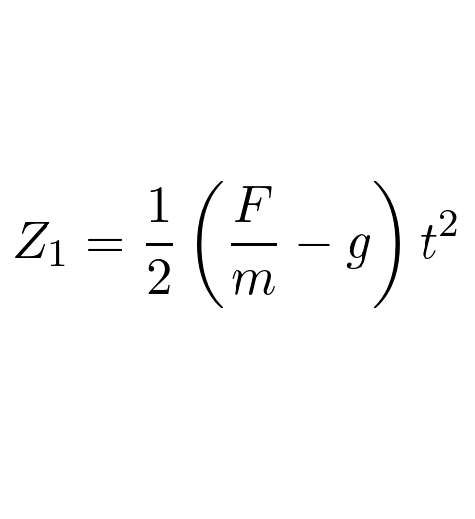
Good Morning! Merry Christmas and Prosperous New Year! I am the leader of the CEFAB group (Brazil). Could you send the “Altitude Calculator Program”‘! Thanks for the help.

Denneth Ahles says:
23rd December 2022 at 15:51
Hello Carlos,
I have not heard of the CEFAB group before, but assume it has something to do amateur rocketry, given the context.
You are free to download the program, at the bottom of the article there is a download link, as well as a link to the source code.
If it does not work, check if you have the correct version of .NET installed, and keep in mind it only runs on Windows.
I would recommend that for any serious design work that you consult a more advanced program such as OpenRocket, or one of the spreadsheets created by Nakka, as this program does not take into account such factors as “stability”, and is for a rough overview only.
If you have any further questions, feel free to ask.
– Denneth
Reply

S	M	T	W	T	F	S
					1	2
3	4	5	6	7	8	9
10	11	12	13	14	15	16
17	18	19	20	21	22	23
24	25	26	27	28	29	30

Rocket Motors Made	30
Rockets launched	4

The Program

The Maths

Downloads

2 thoughts on “Rocket Altitude Estimator”

Leave a Reply Cancel reply